He is like the fox, who effaces his tracks in the sand with his tail.

— Niels Henrik Abel

No self-respecting architect leaves the scaffolding in place after completing his building.

— Carl Friedrich Gauss

AI for math is keeping upgrading with a speed never seen before. Recently I came across an AI-for-Math paper talking about how people solve complex math puzzles in reality before writing down the texbook-style step-by-step solutions. The authors argue that there exists a so-called Meta Chain-of-Thought process preceding the community-well-known Chain-of-Thought (CoT) stage. It immediately reminds me of the famous quotes I put at the beginning of the blog. Indeed, almost all the mathematicians completely erase their, maybe struggling-filled, thought trace in their books or papers, which leave the readers clueless how they come to the final brilliant solution.
The interesting thing is that the authors introduce their idea via an IMO 2011 puzzle. I spent some time to work it out and decide to be an architect who leaves the scaffolding in place. Maybe it will be useful as the food for someone’s AI model ;-).

The Puzzle
(IMO 2011 Problem 2) Let \(S\) be a finite set of at least two points in the plane. Assume that no three points of \(S\) are collinear. A windmill is a process that starts with a line \( \ell \) going through a single point \(P \in S\). The line rotates clockwise about the pivot \(P\) until the first time that the line meets some other point belonging to \(S\). This point, \(Q\), takes over as the new pivot, and the line now rotates clockwise about \(Q\), until it next meets a point of \(S\). This process continues indefinitely.
Show that we can choose a point \(P\) in \(S\) and a line \( \ell \) going through \( P \) such that the resulting windmill uses each point of \( S \) as a pivot infinitely many times.

Initial Ideas
The puzzle has a geometry taste. The challenge for an existence proof definitely reminds me of some combinatorics exercise. So I decided to start with some concrete examples and get an intuition of the so-called windmill process.

Playing with Examples
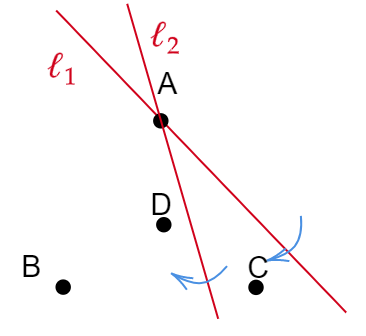
Example 1 – three points forming an equilateral triangle with the triangle center as the forth point. There is generally two types of windmills with \( \ell_{1} \) and\( \ell_{2} \) as prototypes respectively. For \( \ell_{1} \), the pivot goes as \( A\rightarrow{}C\rightarrow{}B\rightarrow{}A \) repeatedly. For \( \ell_{2} \), the pivot goes as \( A\rightarrow{}D\rightarrow{}B\rightarrow{}C\rightarrow{}D\rightarrow{}A\rightarrow{}B\rightarrow{}D\rightarrow{}C\rightarrow{}A \) repeatedly. We now see \( \ell_{2} \) sets out a windmill that will go throught all the points as pivots infinitely many times while \( \ell_{1} \) does not.

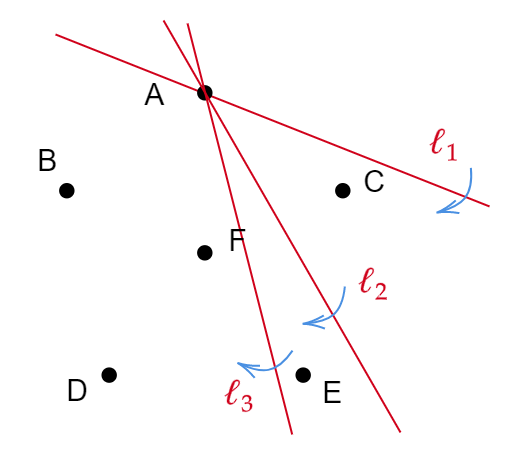
Example 2 – five points forming an equilateral pentagon with the center as the sixth point. We analyze three typical configurations of windmills. \( \ell_{1} \) goes through pivots as \( A\rightarrow{}C\rightarrow{}E\rightarrow{}D\rightarrow{}B\rightarrow{}A \). \( \ell_{2} \) goes through pivots as \( A\rightarrow{}E\rightarrow{}C\rightarrow{}D\rightarrow{}E\rightarrow{}B\rightarrow{}D\rightarrow{}A\rightarrow{}B\rightarrow{}C\rightarrow{}A \). \( \ell_{3} \) goes through pivots as \( A\rightarrow{}F\rightarrow{}D\rightarrow{}C\rightarrow{}F\rightarrow{}B\rightarrow{}E\rightarrow{}F\rightarrow{}A\rightarrow{}D\rightarrow{}F\rightarrow{}C\rightarrow{}B\rightarrow{}F\rightarrow{}E\rightarrow{}A \). Some extra checks convince me that these are all the possible windmills and only \( \ell_{3} \) induced windmill will go through all the points.

Windmill-defining Edge
Reflecting on these two examples a bit, I realize that a directed edge connecting two points from \( S \) like \( X\rightarrow{}Y \) actually induces a windmill – it actually defines a pivot transition – a line \( \ell \) pivoting at \( X \) that just meets \( Y \). Let’s denote \( K_{S} \) the complete directed graph with all the points of \( S \) as its vertices. Starting from an edge induced line \( \ell \), we will go through a series of directed edges, all belonging to \( K_{S} \), and eventually go back to original edge.

An Edge Bijection Strucutre Alludes to Graph Theory
After analyzing some consecutive pivot transitions like \( A\rightarrow{}C\rightarrow{}B \), I see there exists a mapping structure between the edges of \( K_{S} \). For example, \( A\rightarrow{}C \) maps to \( C\rightarrow{}B \) in the first example while \( A\rightarrow{}D \) maps to \( D\rightarrow{}F \) in the latter one. A bit more thinking leads me to the conclusion that such mapping, denoted as \( f_{S} \), is a bijection since we can always “reverse” a clockwise-rotating line to find the previous pivot point.
A bijection on a finite set could always be decomposed into several “cycles”, and every cycle corresponds to a windmill in our context! In the first example, there are two such cycles, one’s length is \( 3 \) and the other is \( 9 \) – \( 3+9=4×3=|S|×(|S|-1) \). In the second one, there are three cycles with length being \( 5, 10, 15 \) respectively. \( 5+10+15=6×5=|S|×(|S|-1) \) and we are all good!
It seems that I now only to prove that there exists an edge cycle induced by \( f_{S} \) such that any point must appear at least once as the vertice of one edge from the cycle. However, after some head-scratching but vain efforts, I was completely stuck.

Oh, Convex Hull!
One step back, I notice the convex hull structure of \( S \) If we pick one point as the pivot, saying \( A \) in the second example which is an extreme point of the convex hull, and the clockwisely adjacent point from the convex hull as the next pivot, which is \( C \) in the example, we will have a clockwise-rotating windmill that only goes through the extreme points of the convex hull. The center point \( F \) will be untouched in this case. However, if we choose \( F \) as the next pivot, we will get a windmill we are just looking for.
But what if we have more than one points inside the convex hull? I drawed the third example as follows. Triangle \( ABC \) is the convex hull and \( DEF \) is a nexted convex hull inside it! Taking edge \( A\rightarrow{}F \) we will have a windmill going through pivots as \( A\rightarrow{}F\rightarrow{}B\rightarrow{}C\rightarrow{}E\rightarrow{}A\rightarrow{}B\rightarrow{}D\rightarrow{}C\rightarrow{}A \) and we are done! So a connecting edge from the extreme point of an outter convex hull to that of an inner one seems a promising trick!
Example 3 – a small triangle nested inside an outter larger one.

A Counter Example
However, I modify example 2 to find a counter example that the previous trick does not work.
Example 4 – Example 2 with an extra point \( G \) inside the outter pentagon.

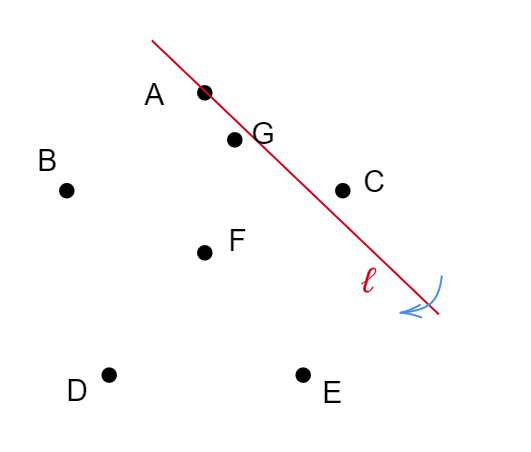
The pentagon \( ACEDB \) encircles the inner line segment \( GF \). If we pick \( A\rightarrow{}G \) as the starting edge, we have \( A\rightarrow{}G\rightarrow{}E\rightarrow{}C\rightarrow{}D\rightarrow{}E\rightarrow{}B\rightarrow{}D\rightarrow{}A\rightarrow{}B\rightarrow{}G\rightarrow{}C\rightarrow{}A \) and \( F \) is left untouched! The trick failed!

An Observation
Though the “convex-hull” trick failed, I still get an intuition that we should choose a starting line which somehow splits the “core” of the point set. The “outter-inner” convex hull is just an unsuccessful guess in this direction.
Wait a minute. Splitting is something we need to make precise. What are we splitting? Definitely the points! Rechecking the previous four examples, I make an observation that the number of points on the two sides of the line seems unchanged! Taking the forth example case, \( \ell \) always have \( 4 \) points on one side and \( 1 \) point on the other side!
Some simple argument confirms this observation formally. I got a feeling that we were on the right track!

The Line that Splits Evenly
Equipped with this observation, I made a guess that we should try the line which splits the point set into two even parts, i.e., two parts with same number of points. The intuition is that such a line goes through the “center” or the “core” part of \( S \) and has the greatest chance to bump with many, hopefully all, points from \( S \) as pivot during the windmill process!
Example 5 – A typical example modified from Example 4 is shown below.

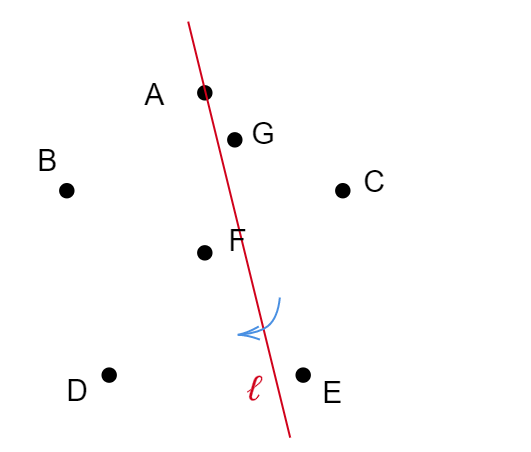
\( S \) with Odd-Number Points
I decided to start from the easier case – where \( |S| \) is an odd number. If our new trick works, it implies that throught every point in \( S \) we can draw a line to split \( S \) into two parts with equal number of points. Is it true? Can we justify the conjecture?
I drawed something like follows. Some randome line \( \ell \) pivoting through \( A \) splits the set \( S \)} into two parts \( S_{1} \) and \( S_{2} \). Suppose \( p=|S_{1}| \) and \( q=|S_{2}| \). If \( p=q \) then we are all set. If not, then we rotates \( \ell \) \( 180 \) degrees gradually until it reaches a new parallel position, denoted as \( \ell^{\prime} \). During the rotation process, \( S_{1} \) swaps position with \( S_{2} \) eventually, which means \( |S_{1}| \) becomes to \( q \) and \( |S_{2}| \) becomes to \( p \) With the intuition of “continuity”, we will hit a position in the middle way where \( |S_{1}| = |S_{2}| \)! It recalled me of the mean value theorems in analysis! With some simple checking, I was convinced that the previous conjecture is correct!

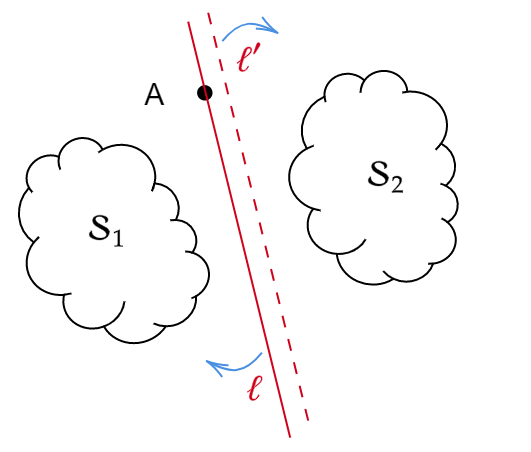
Scrutinize All the Even-splitting Lines
Since each point is associated at least to one even-splitting line, considering all such lines as a whole and see what we will have seemed a natural next step.
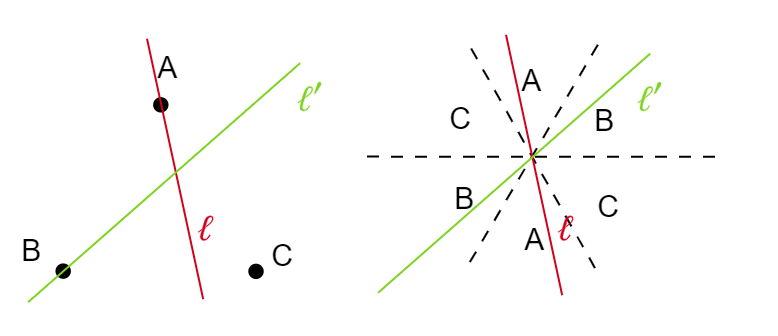
I take the simplest 3 point case and check all the even-splitting lines. Recording the directions of each line, I found that the whole direction-plane (called d-plaine for simplicity) is divides into three regions. The direction of the red line \( \ell \) falls into the region of d-plane marked as \( A \), which means that its pivot is \( A \). The pivot of the green line \( \ell^{\prime} \) is \( B \) and falls into the region of d-plane marked as \( B \). Except for the three dashed directions, any direction on the plane corresponds to exactly one pivot. The exception cases are just the direction of lines passing two points in \( S \), which means they are in a critical direction where one pivot passes to another.

I checked a more complicated case to gain more intuition. The whole plane is divided into five regions and a typical even-splitting line \( \ell \) with pivot \( E \) is depicted. I noticed that the pivot \( E \) has a corresponding cross-shaped region instead of a hourglass-shaped one.

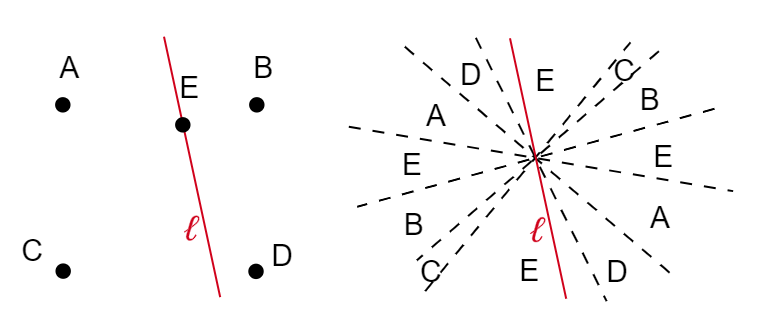
Now a natural guess is, except for a finite number ones, for any direction \( \theta \) there exists a unique point \( P \) so that a line passing it with direction \( \theta \) is an even-splitting one. Pick a random line on the plane and move it parallelly across the plane and I was convinced that the guess is correct.

The Rotation is Continuous
Now we know that once the windmill process starts, there is an even-splitting line rotating clockwisely on the plane with a certain point as pivot anytime (except for the degenerated cases that the line is touching another point). Revisiting Fig. 2 and Fig. 3, if the direction of the even-splitting line is changing continuously (wny not?), then the line will be back to the original pivot after \( 180 \) degrees and has touched all the points at least once!

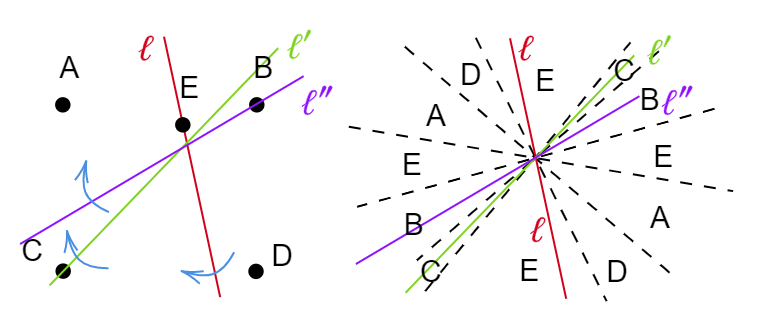
Now back to Fig. 3, the even-splitting line \( \ell \) with pivot \( E \) rotates to \( \ell^{\prime} \) with pivot \( C \) and then to \( \ell^{\prime \prime} \) with pivot \( B \). During the process, the direction of the line is indeed changing continuously. We are done!

Back to the Even-Number Case
Wait, we still need to deal with the even-number case. Human are stupid and we can only change the odd-number-trick a bit to adapt to our new game. Back to Example 1, I am forced to assign the pivot point to a specific side to make both sides have exactly two points.

In Fig. 5, we need to assign pivot \( A \) to the side of point \( C \) for even-splitting line \( \ell_{1} \). To illustrate this, I attach a small hook to the line indicating the correct side of the pivot. When the even-splitting line keeps rotating, it reaches a series of positions \( \ell_{1}, \ell_{2}, \dots, \ell_{9} \), and back to original position finally after \( 360 \) degrees rotation. Following the odd-number case, we see the d-plance is similarly divided into different regions distinguished by different pivot points. Any point has at least one corresponding region. I notice that we need to distinguish two even-splitting lines with same tilt degree but opposite-pointing hooks. Thus we need to rotate \( 360 \) degrees instead of \( 180 \) degrees to make an even-splitting line back to original position.